[!abstract] INTRODUCTION 在自然语言处理（NLP）乃至更广泛的序列数据处理领域，Transformer 架构的兴起无疑是一场革命。它凭借自注意力（Self-Attention）机制并行处理序列中的所有元素，极大地提升了模型训练的效率和性能。然而，这种并行化的设计也带来了一个固有的“缺陷”——它无法感知序列中元素的顺序。对于一个纯粹的自注意力网络而言，“我爱你”和“你爱我”这两个序列的词袋表示是完全相同的，这显然违背了自然语言的逻辑。
为了解决这个问题，需要将元素（token）在序列中的位置编码后送入模型，让模型理解位置关系，也就是位置编码（Positional Encoding, PE）。研究者们提出了各种巧妙方法，本文将从原理、演进、数学推导到前沿进展，深入剖析位置编码的奥秘，并探讨如何设计一个有效的位置编码算法。

Transformer的“顺序失忆症”

自注意力机制的核心是通过计算查询（Query）和键（Key）之间的相似度来为值（Value）分配权重。对于序列中的任意一个词向量 $x_i$，其更新后的表示是序列中所有词向量 $x_j$ 的加权和：

$$\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V$$

在这个计算过程中，无论 $x_i$ 和 $x_j$ 的位置如何交换，只要它们的值不变，它们之间的注意力权重就不会改变。这种特性被称为置换不变性（Permutation Invariance）。这对于很多任务是致命的，因为顺序信息至关重要。

位置编码的使命就是打破这种不变性，为模型提供每个输入元素在序列中的绝对或相对位置信息。它通过创建一个与词嵌入维度相同的向量，然后将其“添加”或“融合”到原始的词嵌入中，使得最终的输入向量既包含语义信息，又包含位置信息。

一般的做法是：通过某种方法获得和原始序列维度相同的PositionEncoding，直接相加：

$$\text{InputEmbedding}_{\text{final}} = \text{TokenEmbedding} + \text{PositionalEncoding}$$ 理论上来说，计算出的位置编码可以以其他方式融入，比如直接在合适的维度上拼接起来，或者做乘法，但确实，这种加性位置编码成为了主流。 #question

从最简单的位置编码思路出发

用整型值标记位置

一种自然而然的想法是，给token增加一个维度来标记位置，第一个token标记1，给第二个token标记2…，以此类推。
这种方法产生了以下几个主要问题：

模型可能遇见比训练时所用的序列更长的序列。不利于模型的泛化。
模型的位置表示是无界的。随着序列长度的增加，位置值会越来越大，不利于模型学习。

用[0,1]范围标记位置

为了解决整型值带来的问题，可以考虑将位置值的范围限制在[0, 1]之内，将token的位置编号归一化。

比如有3个token，那么位置信息就表示成[0, 0.5, 1]；若有四个token，位置信息就表示成[0, 0.33, 0.69, 1]。

但这样产生的问题是：当序列长度不同时，token间的相对距离是不一样的。

用二进制向量标记位置

我们还可以想到用二进制编码。如下图，假设d_model = 3，那么我们的位置向量可以表示成：

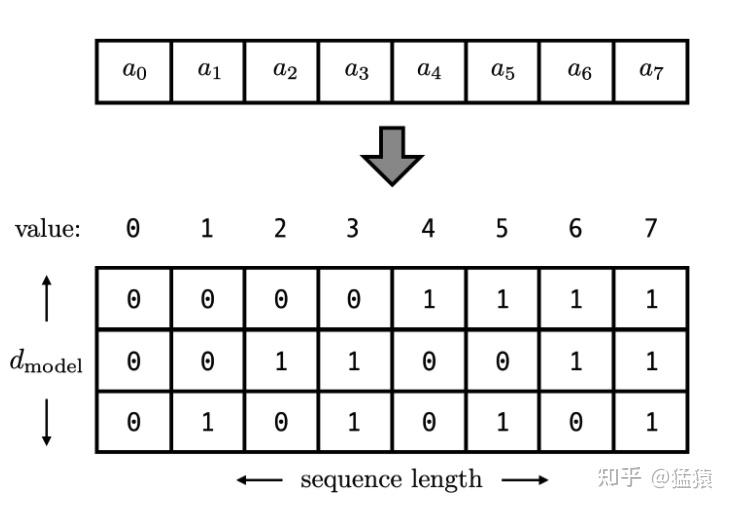
这下所有的值都是有界的（位于0，1之间），且transformer中的 $d_{model}$（论文中采用的256）本来就足够大（$2^{256} \approx 10^{77}$），基本可以把我们要的每一个位置都编码出来了。

但是这种编码方式也存在问题：

二进制位置向量，处在一个离散的空间中，不同位置间的变化是不连续的。
相邻整数的二进制编码的汉明距离、欧式距离、或者余弦相似度都不是等距的，用来位置编码会很反直觉。

[!note] 总结一下，我们希望的好的位置编码应该是：
可以表示一个token在序列中的绝对位置
在序列长度不同的情况下，不同序列中token的相对位置/距离也要保持一致
可以外推，用来表示模型在训练过程中从来没有看到过的句子长度
相邻的位置编码的向量最好是连续的

如何设计一个好的位置编码？

掌握了现有方法的优劣和原理后，我们可以总结出设计一个新的位置编码算法时需要考虑的核心原则和思路。

核心原则

唯一性 (Uniqueness): 必须为序列中的每个位置提供一个独特的信号。
可解释性与不变性 (Interpretability & Invariance): 编码应该易于模型理解。例如，相对距离的编码不应随绝对位置的变化而剧烈变化。
外推性 (Extrapolation): 算法应能优雅地处理比训练时更长的序列。这是可学习位置编码的主要痛点。
效率 (Efficiency): 计算不应成为模型的瓶颈，尤其是在处理长序列时。

设计思路

从绝对到相对: 思考你的任务更依赖绝对位置还是相对位置。大多数现代方法都倾向于直接或间接地建模相对位置。
连续性与平滑性: 相邻位置的编码向量是否应该相似？正弦编码保证了这一点，这有助于模型泛化。
多尺度信息: 正如正弦编码使用不同频率的波来捕捉不同尺度的位置信息一样，一个好的位置编码应该能同时表达粗粒度和细粒度的位置概念。
与注意力机制的融合方式: 位置信息不一定非要和词嵌入相加。它可以被用作注意力的偏置项（Bias），或者以更复杂的方式融入到 Query 和 Key 的计算中。

经典正弦位置编码（Sinusoidal PE）

原始 Transformer 论文提出的正弦位置编码堪称经典，其设计充满了数学之美。理解它的原理对于我们设计自己的位置编码至关重要。

论文中说到，PE的选择有很多——可学习的或者固定的。采用Sinusoidal PE，主要是因为：

论文假设线性的相对位置距离变化可以帮助模型更好的学习，这个公式是满足的；
这个公式理论上可以外推，比可学习的位置编码不能外推要好。 ![[Pasted image 20250829175825.png]]

数学公式

对于位置为 $pos$、维度为 $i$ 的编码值，其计算公式如下：

$$PE_{(pos, 2i)} = \sin\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right)$$

$$PE_{(pos, 2i+1)} = \cos\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right)$$

其中：

$pos$ 是词在序列中的位置（从 0 开始）。
$i$ 是编码向量中的维度索引（从 0 开始，到 $d_{\text{model}}/2 - 1$）。
$d_{\text{model}}$ 是嵌入向量的维度。

设计思想与性质

为什么选择这样一组看似复杂的三角函数？因为它具备以下几个绝佳的性质：

唯一性: 每个位置 $pos$ 都有一个独一无二的位置编码向量。这是因为不同频率的正弦/余弦波组合可以形成唯一的信号。
确定性与高效性: 编码是固定的，可以直接计算得出，无需训练。
对长序列的泛化能力: 即使序列长度超过训练时的最大长度，也能生成有效的位置编码。
蕴含相对位置信息: 这是最精妙的一点。对于任意固定的偏移量 $k$， $PE_{pos+k}$ 可以表示为 $PE_{pos}$ 的一个线性变换。这意味着模型可以轻易地学习到词与词之间的相对位置关系。

让我们来推导一下这个线性变换关系。根据三角函数的和差角公式： $\sin(A+B) = \sin(A)\cos(B) + \cos(A)\sin(B)$ $\cos(A+B) = \cos(A)\cos(B) - \sin(A)\sin(B)$

令 $\theta = \frac{pos}{10000^{2i/d_{\text{model}}}}$ 和 $\phi = \frac{k}{10000^{2i/d_{\text{model}}}}$，则：

$$PE_{(pos+k, 2i)} = \sin(\theta + \phi) = \sin(\theta)\cos(\phi) + \cos(\theta)\sin(\phi)$$ $$PE_{(pos+k, 2i+1)} = \cos(\theta + \phi) = \cos(\theta)\cos(\phi) - \sin(\theta)\sin(\phi)$$

这可以写成矩阵乘法形式：

$$\begin{pmatrix} PE_{(pos+k, 2i)} \ PE_{(pos+k, 2i+1)} \end{pmatrix} = \begin{pmatrix} \cos(\phi) & \sin(\phi) \ -\sin(\phi) & \cos(\phi) \end{pmatrix} \begin{pmatrix} \sin(\theta) \ \cos(\theta) \end{pmatrix} = M_k \begin{pmatrix} PE_{(pos, 2i)} \ PE_{(pos, 2i+1)} \end{pmatrix}$$

可以看到，$PE_{pos+k}$ 的每一对 $(2i, 2i+1)$ 维度都可以通过乘以一个只与偏移量 $k$ 相关的旋转矩阵 $M_k$ 从 $PE_{pos}$ 得到。由于这个变换矩阵 $M_k$ 对于所有位置 $pos$ 都是相同的，模型可以非常容易地学会捕捉这种相对位置关系。

五、前沿进展：旋转位置编码（RoPE）及其他

近年来，位置编码领域涌现出许多优秀的工作，其中**旋转位置编码（Rotary Positional Encoding, RoPE）**尤为引人注目，并已成为 LLaMA 等主流大语言模型的标配。

旋转位置编码 (RoPE)

核心思想: RoPE不再将位置信息“加”到词嵌入中，而是通过“旋转”的方式将其融合进去。它利用了复数的思想，将词嵌入向量 $x_q$ 和 $x_k$ 的每两个维度看作一个复数，然后乘以一个代表位置的旋转矩阵（一个复数 $e^{im\theta}$）。
数学原理: 对于一个位置为 $m$ 的向量 $q_m$，其旋转后的向量 $q’_m$ 为：
$$ $$$$q’_m = f(q, m) = q e^{im\theta}
$$ $$$$当计算两个位置 $m$ 和 $n$ 的向量的内积（注意力得分的关键）时：
$$ $$$$(q’_m)^T (k’_n) = \text{Re}[ (q e^{im\theta})^* (k e^{in\theta}) ] = \text{Re}[ q^*k e^{-i(m-n)\theta} ]
$$ $$$$可以看到，内积的结果只与原始向量 $q, k$ 和它们的相对位置 $m-n$ 有关，与绝对位置 $m, n$ 无关。
优势: RoPE 以一种极其优雅的方式将相对位置信息编码到了自注意力机制中，同时具备良好的外推性。

其他前沿方法

ALiBi (Attention with Linear Biases): 一种更简单但非常有效的方法。它不修改词嵌入，而是在计算注意力分数后，直接给每个分数加上一个与位置距离成反比的惩罚项（偏置）。距离越远的词，其注意力分数受到的惩罚就越大。这种方法极其简单，且表现出了惊人的外推能力。

实践指南：代码实现与使用

下面我们用 PyTorch 实现一个经典的正弦位置编码模块。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
import torch
import torch.nn as nn
import math

class PositionalEncoding(nn.Module):
    def __init__(self, d_model: int, dropout: float = 0.1, max_len: int = 5000):
        """
        经典的 Transformer 正弦位置编码

        Args:
            d_model (int): 模型的维度 (词嵌入维度)
            dropout (float): Dropout 比率
            max_len (int): 预先计算的最大序列长度
        """
        super().__init__()
        self.dropout = nn.Dropout(p=dropout)

        # 创建一个足够长的位置编码矩阵
        pe = torch.zeros(max_len, d_model)
        
        # 位置索引 (0, 1, 2, ..., max_len-1)
        position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)
        
        # 计算除法项的分母，使用 log 空间可以防止数值不稳定
        div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model))
        
        # 计算偶数维度的 sin 值
        pe[:, 0::2] = torch.sin(position * div_term)
        
        # 计算奇数维度的 cos 值
        pe[:, 1::2] = torch.cos(position * div_term)
        
        # 增加一个 batch 维度，使其能够与输入 (batch_size, seq_len, d_model) 相加
        pe = pe.unsqueeze(0)
        
        # 将 pe 注册为 buffer，这样它就不会被视为模型参数，但会随模型移动 (e.g., to(device))
        self.register_buffer('pe', pe)

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        """
        将位置编码添加到输入张量中

        Args:
            x (torch.Tensor): 输入张量，形状为 (batch_size, seq_len, d_model)

        Returns:
            torch.Tensor: 添加了位置编码后的张量
        """
        # x.size(1) 是序列的实际长度
        # self.pe 的形状是 (1, max_len, d_model)，切片后得到 (1, seq_len, d_model)
        x = x + self.pe[:, :x.size(1)]
        return self.dropout(x)

# 如何在模型中使用
d_model = 512
vocab_size = 10000
seq_len = 100

embedding = nn.Embedding(vocab_size, d_model)
pos_encoder = PositionalEncoding(d_model)

# 假设 input_ids 是一个 (batch_size, seq_len) 的张量
input_ids = torch.randint(0, vocab_size, (8, seq_len))

# 1. 获取词嵌入
word_embeddings = embedding(input_ids) * math.sqrt(d_model) # Transformer 论文中的缩放操作
# 2. 添加位置编码
final_embeddings = pos_encoder(word_embeddings)

print(f"输入形状: {word_embeddings.shape}")
print(f"添加位置编码后的形状: {final_embeddings.shape}")

总结与展望

位置编码的演进：从简单到精妙

位置编码并非只有一种形态，它的发展经历了从简单到复杂，从绝对到相对的演进过程。

可学习的绝对位置编码 (Learned Absolute Positional Encoding)
- 思路: 最直观的方法是为每个位置创建一个可学习的嵌入向量。假设序列最大长度为 $L_{max}$，嵌入维度为 $d_{model}$，我们可以创建一个形状为 $(L_{max}, d_{model})$ 的位置嵌入矩阵。在训练过程中，模型会像学习词嵌入一样，自动学习出每个位置的最佳表达。
- 代表模型: BERT, GPT-2。
- 优点: 简单、有效，能够很好地适应特定任务的数据分布。
- 缺点:
  - 泛化性差: 无法处理比训练时所设定的 $L_{max}$ 更长的序列。
  - 数据依赖: 需要大量数据才能学习到有效的位置表示。
固定的绝对位置编码 (Fixed Absolute Positional Encoding)
- 思路: 使用一个固定的、预先设计好的函数来生成位置编码，无需学习。
- 代表模型: 原始 Transformer 论文中提出的正弦/余弦位置编码。
- 优点:
  - 可外推: 理论上可以处理任意长度的序列。
  - 确定性: 无需训练，节省了参数和计算。
- 缺点: 虽然理论上可外推，但在极长的序列上效果可能会下降。
相对位置编码 (Relative Positional Encoding)
- 思路: 核心观点是，模型关注的可能不是一个词的绝对位置，而是两个词之间的相对距离。例如，在计算词 $i$ 对词 $j$ 的注意力时，直接将它们之间的相对位置 $j-i$ 编码进去。
- 代表模型: Transformer-XL, T5, DeBERTa。
- 优点: 对位置关系的建模更直观，在很多任务上被证明比绝对位置编码更有效。
- 缺点: 实现相对复杂，需要在自注意力机制内部进行修改。位置编码是理解现代序列处理模型（尤其是 Transformer）的关键一环。它巧妙地解决了自注意力机制的“顺序失忆症”，为模型注入了时序的概念。

从演进看: 我们见证了从可学习的绝对编码到固定的、数学上更优美的正弦编码，再到如今大放异彩的相对位置编码（如 RoPE）的转变。这一趋势表明，对“相对关系”的建模正变得越来越重要。
从设计看: 一个优秀的位置编码方案需要在唯一性、外推性、效率和与模型架构的契合度之间做出权衡。RoPE 的成功告诉我们，将位置信息以“乘法”或“旋转”等更动态的方式融入计算，可能比简单的“加法”更有效。
未来展望: 位置编码的研究远未结束。对于非线性、非连续的序列数据（如图、多模态数据），如何设计有效的位置（或结构）编码仍然是一个开放且活跃的研究领域。我们可能会看到更多自适应、甚至由模型自身动态生成的位置编码方案。

掌握位置编码的原理，不仅能帮助我们更深入地理解现有模型，更能启发我们在面对新的序列数据和模型架构时，设计出更具创新性的解决方案。

引用

https://zhuanlan.zhihu.com/p/454482273

Transformer的“顺序失忆症”

从最简单的位置编码思路出发

用整型值标记位置

用[0,1]范围标记位置

用二进制向量标记位置

如何设计一个好的位置编码？

核心原则

设计思路

经典正弦位置编码（Sinusoidal PE）

数学公式

设计思想与性质

五、前沿进展：旋转位置编码（RoPE）及其他

旋转位置编码 (RoPE)

其他前沿方法

实践指南：代码实现与使用

总结与展望

位置编码的演进：从简单到精妙

推荐学习资源

引用

💬 评论

Transformer的“顺序失忆症”

从最简单的位置编码思路出发

用整型值标记位置

用[0,1]范围标记位置

用二进制向量标记位置

如何设计一个好的位置编码？

核心原则

设计思路

经典正弦位置编码（Sinusoidal PE）

数学公式

设计思想与性质

五、 前沿进展：旋转位置编码（RoPE）及其他

旋转位置编码 (RoPE)

其他前沿方法

实践指南：代码实现与使用

总结与展望

位置编码的演进：从简单到精妙

推荐学习资源

引用

💬 评论

五、前沿进展：旋转位置编码（RoPE）及其他